所谓九宫格式图片排布,就是把一张图切成九张,以便在常见社交媒体的时间流中抢占最大的版面(不熟悉九宫格布局的读者,可在 banner 中看到实际效果);朋友圈中也有用心人,会以九宫格形式发图。前几年设计图片拼接 Shortcuts 动作时,我顺手做了九宫格拼图功能,以便将别人发的九张图恢复回完整照片。
这类图片,拼起来容易,做起来却不简单,因为需要把一张图等比例切成九张,多数人一听到数字就连连摇头了。也无怪乎,为何一些后期软件内置的切图功能会受到欢迎。不过,Shortcuts 本身就有切图(Crop)功能,只需一点数学技巧,就能打造出效果实用而过程优美的自动化动作。
如何使用
九宫格切图,最后一定是希望获得九张正方形图片,方能展示成 3x3 的矩阵。论其操作,倒也简单,无非是准备好正方形的图片素材,然后让软件负责切割。我设计的动作高度自动化,您只要选择照片,然后稍作调整、将其改为正方形图片,后面的事情全部交给 Shortcuts。
详言之,选择图片后,Shortcuts 会显示一个精简的图片编辑界面(实际上是叠放界面),中间是一个正方形的画布,视原始图片的情况可选择以下操作:
- 图片本身就是正方形,此时稍稍缩放一下,让其边缘与画布边缘差不多对其即可;
- 图片不是正方形,想要展示的也只是其一部分,就可以进一步抻大,让多余部分溢出画布——此时,留下的部分就是一分不多一分不少的正方形;
- 图片不是正方形,但想要完整展示,此时需要给图片配一个底图,就像拍立得相机的相纸一样,此时也仅需要缩放、移动图像,挪到合适的位置——当然,即便是正方形的图片,也有人希望配上边框,让它看上去有相纸风格,此时同样只需调整图片位置和尺寸。

以上三种情形,均可在同一个操作中完成,不需要设置一系列复杂的 If 判断模块,大大降低了 Shortcuts 动作本身的复杂性。有很多 Shortcuts 动作,为了照顾不同的用户,内置了各种功能,结果就是步骤无比冗长、难以维护,甚至设计者自己都看不懂;另一个极端则是学福特汽车:您可以使用任何功能,只要您想要的只是我们提供的这一个功能。如果在设计上就能解决问题,最好不要陷入艰难的选择环节。
确定好需要切分的图片后,视图片大小,在几秒内即可获得切分好的图片。早期的相片店常用“立等可取”之广告,标榜自己冲印速度快;而本动作,可算是实打实的“立等可取”了。
简析原理
要用 Shortcuts 切图不难,难的是如何把这件事儿做得不要那么蠢。前文已经提及,仅仅是准备素材这一步,就要考虑多种情形,而传统做法是塞一大堆的 If 模块。其实,自 iOS 14 开始,Shortcuts 就引入了一个不起眼但威力十足的模块:Calculate Expression。它支持部分 BSD 算式以及部分 Apple 自己的表达式,用它处理涉及数字的内容,就不用一个接一个地组合 Shortcuts 计算模块。我曾在会员栏目中介绍过 PDF 下载动作,它还有个自动裁剪页面的增强版,就用到了算式。
切图时,我也引入了大量算式,把原本可能要几十步的动作压缩到仅仅十几步,大大降低后期维护成本。如波利亚所言,链条的强度取决于其最薄弱的环节,而一个几十步甚至上百步的动作,可能会留下太多弱点,以至于你都不知道哪一步出了问题。
用算式找出图片的长边
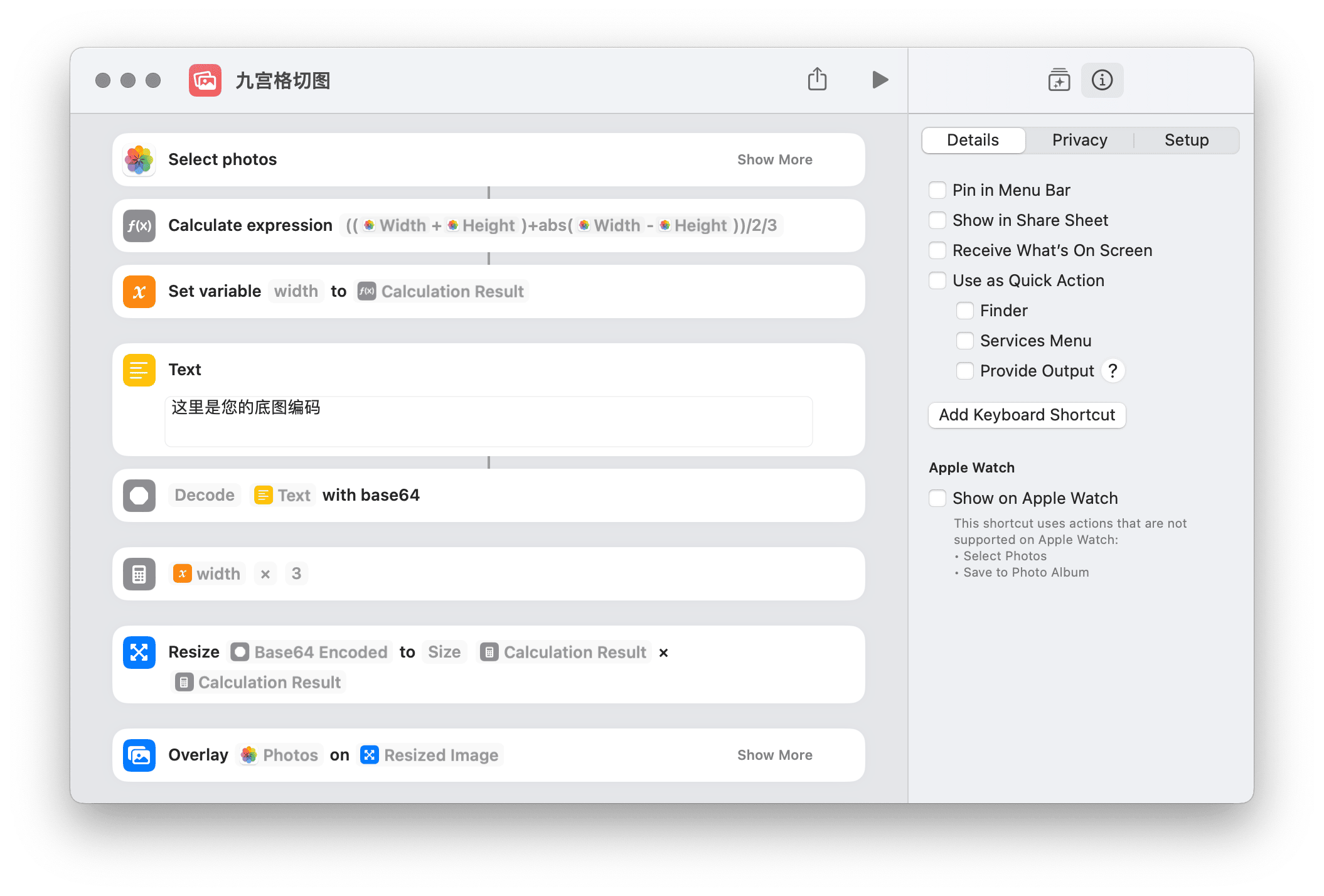
注意:就比对图片长宽这一步而言,Shortcuts 已经有计算最大值的模块,我自行编写算式是为了减少 Shortcuts 步骤,三五步减少到一步,不过必要性诚然不大——主要是一种乐趣。正如特斯勒复杂守恒定律所揭示的,只是把 Shortcuts 动作的复杂性转移到算式上,复杂本身并未消失。动作一开始,Shortcuts 会准备一张底图(以 base64 编码形式存储,可用此动作将您自己准备的图片编码),并以原图的长边为变长,将底图其调整为 长边x长边 的正方形。而输入的图片既可能是高度更长,也可能是宽度更大,需要判断。我写了一个算式,用基础算术即可算出长边的数值。下面的完整算式还将长边除以 3,得出的是切分后的小正方形图片边长。
((Photos Width+Photos Height)+abs(Photos Width-Photos Height))/2/3
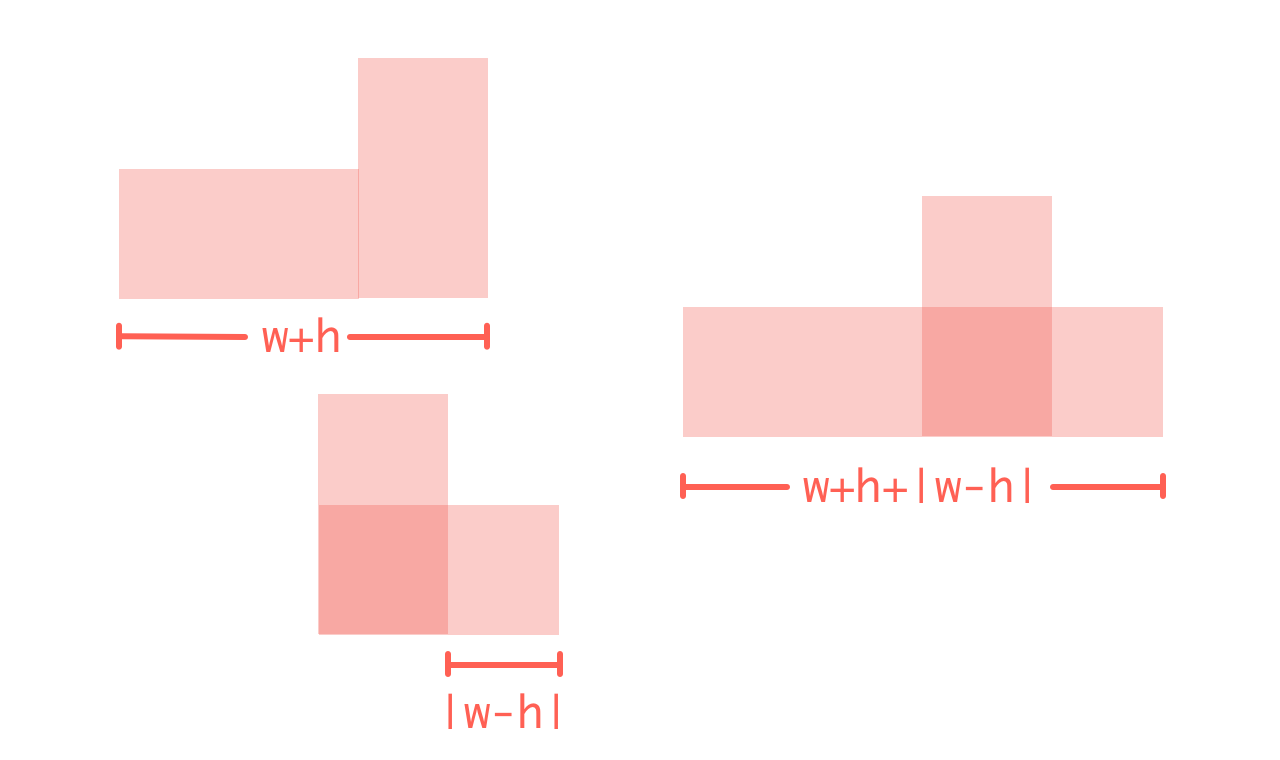
换成几何图示比较好理解,长加宽,再加上长宽的差,刚好就是两个长边;将其除以 2,就得到了长边的值。
用算式确定切图位置
接下来,要准备切图工作。切图有两组参数,一组是开始切图的座标,另一组是切分所得图片的长宽,后者刚刚已经算出来了,只需直接填上;现在的问题,是如何确定起始座标。1稍微观察一下每一次切图的座标位置(单位座标),不难发现,其中必有规律。
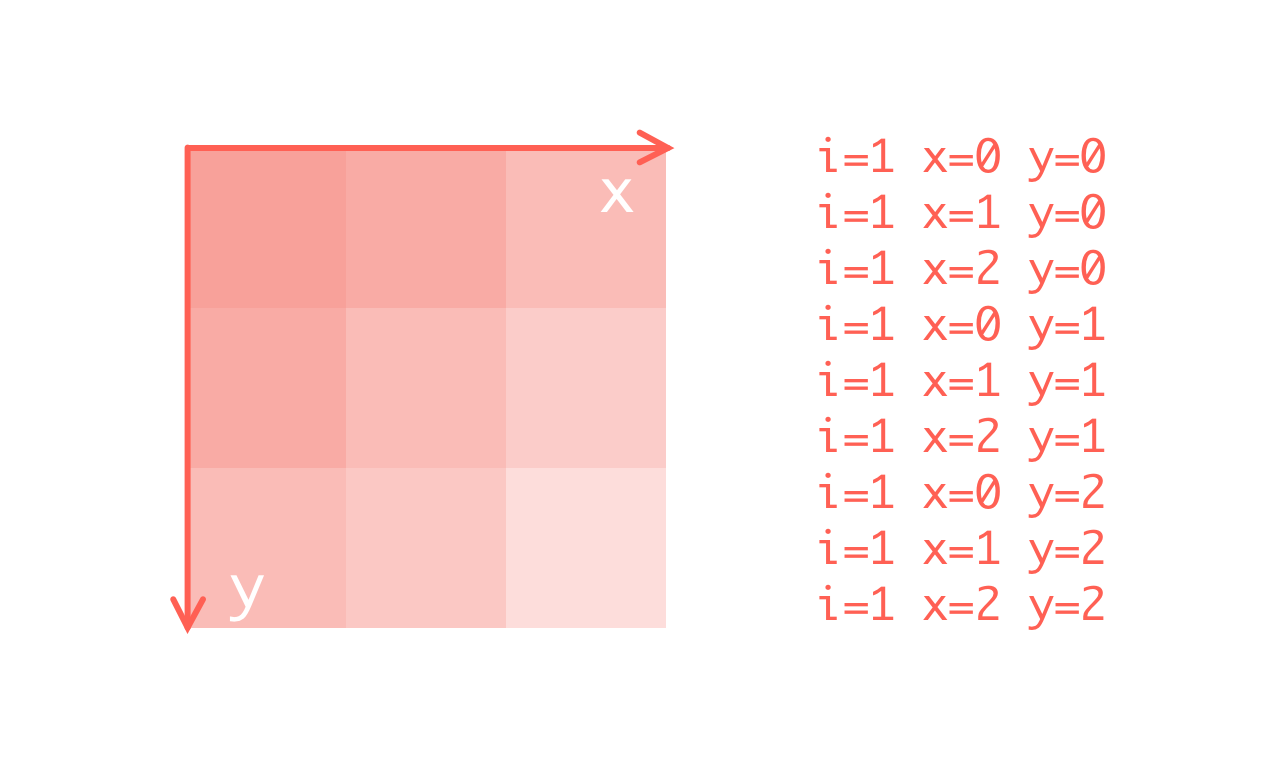
具体推导过程此处略去,突破口在于 3 这个数字,无论横竖座标,均每三次出现一轮更迭,而对应的算子一般就是取余 mod 和最常见的除法。稍加归纳,计算座标轴的算式就出来了:
- 计算 x 座标:
(Repeat Index+2)mod3*width - 计算 y 座标:
rint((Repeat Index-2)/3)*width2
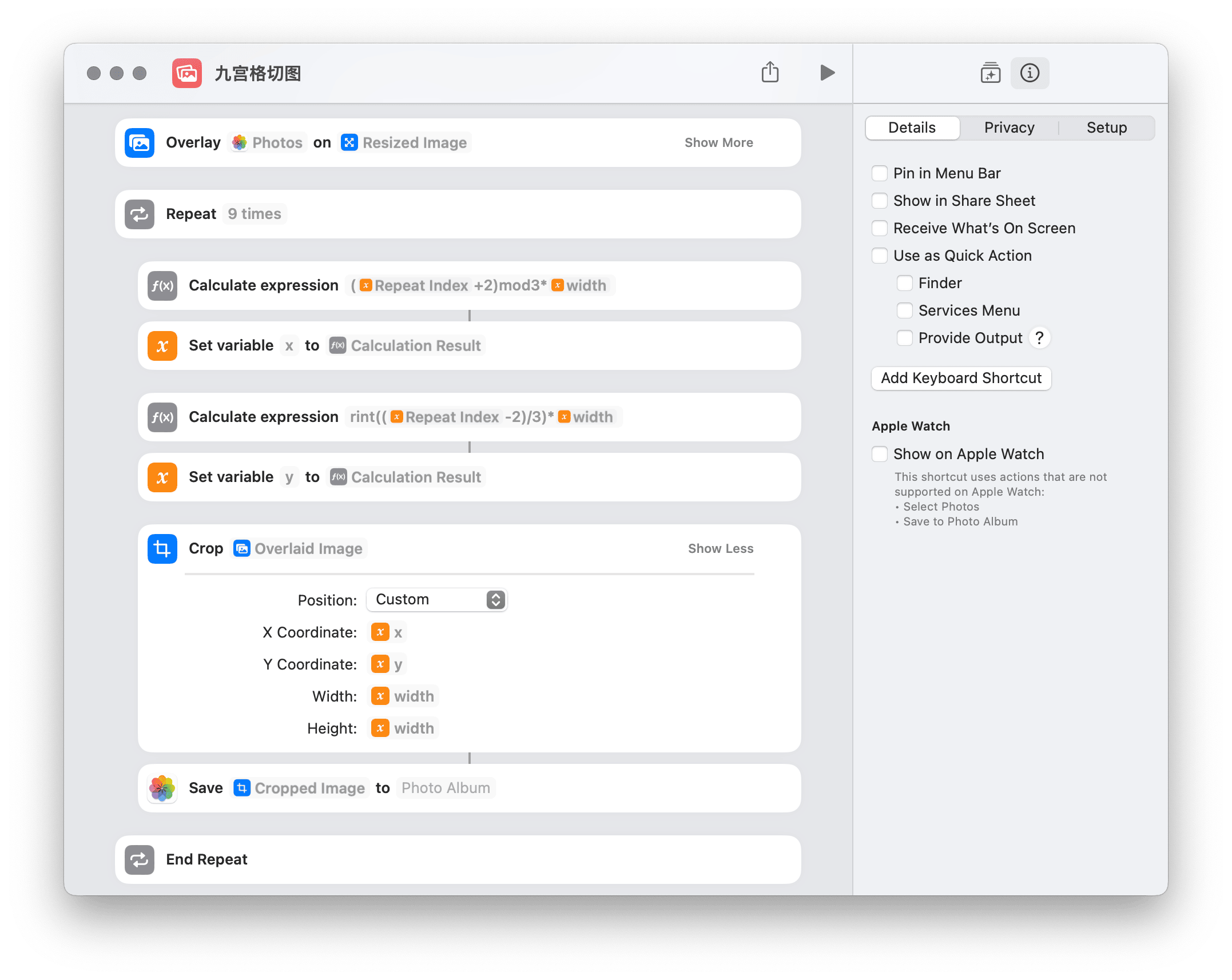
小结
Shortcuts 并非寻常意义上的软件(Application),它不是传统的生产-消费模式,而是让用户自己制作工具。因此,制作过程也是软件体验的一部分,涉及一个 Shortcuts 动作的内部“工艺”是否精巧,是否易于理解,是否便于维护。
Shortcuts 有不少模块——例如正则表达式匹配、URL Scheme 和 Javascript——属于通用工具,在大大缩减对图形化界面之依赖的同时,也便于调试,不需要揣测 Apple 的设计师埋了什么新品种地雷或留了什么祖传未爆弹。相比之下,对于算式模块的关注则太少了,本文借九宫格切图这一涉及大量计算的场景,一探 Shortcuts 中的算式与数学。
就像 Jobs 监督制造苹果电脑时说的那样,工具的内部结构,用户或许看不到,但设计者看得到,制作者看得到,上帝看得到。

